Software Testing Methodologies Dichotomies

Strategies in Data Flow Testing are:

All-du Paths (ADUP)
The all-du-paths strategy is the strongest data flow testing strategy
It requires that every du path form every definition of every variable to every use of that definition be exercise under some test
For variable X
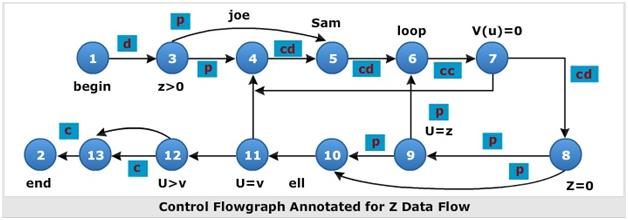
In image, because variable X are used only on link (1, 3) any test that starts at the entry satisfies this criterion (for variable X, but not for all variables as required by the strategy)

For Variable z
The situation for variable z (image) is more complicated because the variable is redefined in many places
For the definition on link (1, 3) we must exercise paths that include sub paths (1, 3, 4) and (1, 3, 5)
The definition on link (4, 5) is covered by any path that includes (5, 6) such as sub path (1, 3, 4, 5, 6 ....)
The (5, 6) definition requires paths that include sub paths (5, 6, 7 and 4) and (5, 6, 7 and 8)

For variable v
Variable V (image) is defined only once on link (1, 3)
Because V has a predicate use at node 12 and the subsequent path to the end must be forced for both directions at node 12, the all-du-paths strategy for this variable requires that we exercise all loop-free entry/exit paths and at least one path that includes the loop caused by (11, 4)
Note that we must test paths that include both sub paths (3, 4, 5) and (3, 5) even though neither of these has V definition
They must be included because they provide alternate du paths to the V se on link (5, 6)
Although (7, 4) is not used in the test set for variable V, it will be included in the test set that covers the predicate uses of array variable v() and U
The all-du-paths strategy is a strong criterion, but it does not take as many tests as it might seem at first because any one test simultaneously satisfies the criterion for several definitions and uses of several different variables

All Uses Strategy (AU)
The all uses strategy is that at least one definition clear path from every definition of every variable to every use of that definition be exercised under some test
Just as we reduced our ambitions by stepping down from all paths (P) to branch coverage (C2), say, we can reduce the number of test cases by asking that the test set should include at least one path segment from every definition to every use that can be reached by that definition

For Variable V
In image, ADUP requires that we include sub paths (3,4,5) and (3,5) in some tests because subsequent uses of V, such as on link (5,6) can be reached by either alternative
In AU, either (3,4,5) or (3,5) can be used to start paths, but we don't have to use both
Similarly, we can skip the (8,10) link if we've included the (8,9,10) sub path
Note the hole, we must include (8,9,10) in some test cases because that's the only way to reach the c use at link (9,10-) but suppose our bug for variable V is on link (8,10) after all? Find a covering set of paths under AU for the image shown below

All p-uses/some c-uses strategy (APU + C)

For every variable and every definition of that variable, include at least one definition free path from the definition to every predicate use

If there are definitions of the variables that are not covered by the above prescription, and then add computational use test cases as required to cover every definition

For variable Z

In image for APU + C we can select paths that all take the upper link (12, 13) and therefore we do not cover the c-use of Z but that's okay according to the strategy's definition because every definition is covered

Links (1,3), (4,5), (5,6) and (7,8) must be included because they contain definitions for variable z

Links (3,4), (3,5), (8,9) (8,10), (9,6) and (9,10) must be included because they contain predicate uses of Z

Find a covering set of test cases under APU + C for a ll variables in this example - it only takes two test

For variable V

In image, APU + C is achieved for V by (135678, 10,11,4,5,6,7,8,10,11,12[upper],13,2) and (1,3,5,6,7,8,10,11,12[lower], 13,2)

Note that the c-use at (9,10) need not be included under the APU + C criterion

All c-uses/some p-uses strategy (ACU + P)

The all c-uses/some p-uses strategy (ACU+P) is to first ensure coverage by computational use cases

If any definition is not covered by the previously selected paths, add such predicate use cases as are needed to assure that every definition is included in some test

For variable z

In image ACU + P coverage is achieved for Z by path (1,3,4,5,6,7,8,10,11,12,13[lower], 2) but the predicate uses of several definition are not covered

Specifically, the (1,3) definition is not covered for the (3,5) p-use, the (7,8) definition is not covered for the (8,9), (9,6) and (9,10) p-uses

The above examples imply that APU+C is stronger than branch coverage, but ACU+P may be weaker than, or incomparable to branch coverage

All Definition Strategy (AD)
the 'all definitions strategy' reveals that every definition of every variable be covered by at least one use of that variable; be it the use a computational use or a predicate use.
For variable Z
Path(1,3,4,5,6,7,7....) satisfies this criterion for variable Z, whereas any entry/exit path satisfies it for variable V
From the definition of this strategy we would expect it to be weaker than both ACU +P and APU+C

All Predicate Uses (APU), All Computational Uses (ACU) Strategies
The 'all predicate uses strategy' is derived from APU+C strategy by dropping the requirement that we include a c-use for the variable if there are no p-uses for the variable
The 'all computational uses strategy' is derived form ACU+P strategy by dropping the requirement that we include a p-use for the vaiable if there are no c-uses for the variable
It is obvious that ACU should be weaker than ACU+P, and APU should be weaker than APU+C